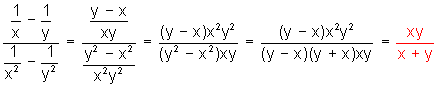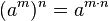Inicio | DOCUMENTOS NOVENO

DOCUMENTOS PARA EL CUARTO PERÍODO

Potencias en el conjunto de los números reales.docx (212823)

ALGUNOS CONCEPTOS BÁSICOS

Una potencia es una forma abreviada de escribir un producto de factores iguales.

Por ejemplo, si queremos multiplicar el número 3 cinco veces podemos escribir el siguiente producto de factores.

3 . 3 . 3 . 3 . 3 = 243

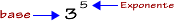
Sin embargo, esta forma de expresar este tipo de operaciones es tediosa y poco práctica. Una manera más sencilla es hacerlo forma de potencia.

Una potencia consta de dos partes, por un lado está la base que es el número que se multiplica por sí mismo, es decir el FACTOR y por otro el EXPONENTE que nos indica el número de veces que se multiplica el número.

Para tener en cuenta:

Las potencias de exponentes dos y tres se denominan respectivamente cuadrados y cubos perfectos.

Acá les dejo algunos enlaces para que practiquen:

Para empezar: https://www.isftic.mepsyd.es/w3/eos/MaterialesEducativos/primaria/matematicas/conmates/unid-5/potencias.htm
Expresar en forma de potencia https://www.ematematicas.net/potencia.php
Para leer potencias correctamente https://www.juntadeandalucia.es/averroes/centros-tic/11700160/helvia/aula/archivos/repositorio/0/187/html/1ESO/index.html
Calcular la potencia https://www.juntadeandalucia.es/averroes/recursos_informaticos/proyectos2004/matematicas/Tema1/MulDivPot.htm
Identificar valores de potencias https://www.juntadeandalucia.es/averroes/recursos_informaticos/proyectos2004/matematicas/Tema1/MulDivPot.htm
Cuadrados y cubos perfectos https://descartes.cnice.mec.es/materiales_didacticos/Potencias_y_raices/potencias1.htm
Elementos de las potencias, cuadrados y cubos pefectos https://www.aplicaciones.info/decimales/poten01.htm

PROPIEDADES DE LA POTENCIACIÓN

Multiplicación de potencias de igual base

El producto de dos o más potencias de igual a base «a» es igual a la potencia de base a y exponente igual a la suma de los exponentes respectivos.

$a^m \cdot a^n = a^{m + n}$

ejemplos:

$9^3 \cdot 9^2 = 9^{3+2}= 9^5$

División de Potencias de Igual Base

La división de dos potencias de igual base a es igual a la potencia de base a y exponente igual a la resta de los exponentes respectivos (la misma base y se restan los exponentes.

$\frac{a^m}{a^n}=a^{m - n}$

Potencia de una potencia

La potencia de una potencia de base a es igual a la potencia de base a elevada a la multiplicación de ambos exponentes -

$(a^m)^n = a^{m \cdot n}$

Potencia de base 10

En las potencias con base 10, el resultado será la unidad seguida de tantos ceros como indica la cifra del exponente.

Ejemplos:

$10^0=1 \,$

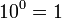
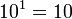
$10^1=10 \,$

$10^2=100 \,$

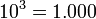
$10^3=1.000 \,$

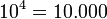
$10^4=10.000 \,$

$10^5=100.000 \,$

$10^6=1.000.000 \,$

Potencia de un producto

La potencia de un producto es igual a cada uno de los factores del producto elevados al exponente de dicha potencia. Es decir, una potencia de base (a.b) y de exponente "n", es igual al factor "a" elevado a "n" por el factor "b" elevado a "n"

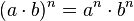
$(a \cdot b)^n=a^n \cdot b^n$

Propiedad distributiva

La potenciación es distributiva con respecto a la multiplicación y a la división:

$(a \cdot b)^n = a^n \cdot b^n$

$\Big(\frac{a}{b}\Big)^n = \frac{a^n}{b^n}$

pero no lo es con respecto a la suma ni a la resta.

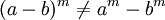
$(a + b)^m \neq a^m + b^m$

$(a - b)^m \neq a^m - b^m$

Acá les dejo unas actividades para practicar PROPIEDADES DE LA POTENCIACIÓN

y acá hay una linda página para profundizar... fijate en el menú de la izquierda .....LA POTENCIA Y SUS PROPIEDADES

PUNTO PENDIENTE

PARA RECUPERAR MATEMÁTICAS NECESITAN HACER LO SIGUIENTE:

1. Biografía de los Referentes Matemáticos, Valor 30%:

Elaborar un trabajo en diapositivas (power point) sobre estos matemáticos:

Euler, Gauss, Thales, Jhon Neper

2. Talleres de recuperación de Matemáticas, Valor 40%

TALLERES DE MATEMÁTICAS

TALLER DE RECUPERACION DE MATEMÁTICAS (1) 9º.docx (22949)

TALLER DE RECUPERACIÓN DE MATEMÁTICAS (2) 9º.docx (23402)

TALLER DE RECUPERACION DE MATEMÁTICAS (3) 9º.docx (27285)

TALLER DE RECUPERACIÓN DE MATEMÁTICAS (4) 9º.docx (31776)

3. SUSTENTACIÓN DE LOS TALLERES Y EL TRABAJO. VALOR 30%

DOCUMENTOS NOVENO

Para el tema de sistemas de ecuaciones lineales se recomienda mirar el archivo adjunto.

Sistemas de Ecuaciones Lineales.docx (75,7 kB)

FUNCIÓN LINEAL

Una función lineal es una función cuyo dominio son todos los números reales, cuyo codominio también todos los números reales, y cuya expresión analítica es un polinomio de primer grado.

La función lineal se define por la ecuación f(x) = mx + b ó y = mx + b llamada ecuación canónica, en donde m es la pendiente de la recta y b es el intercepto con el eje Y.

Por ejemplo, son funciones lineales f(x) = 3x + 2 g(x) = - x + 7 h(x) = 4 (en esta m = 0 por lo que 0x no se pone en la ecuación).

Esta es la gráfica de la función lineal y = 3x + 2

Vemos que m = 3 y b = 2 (de la forma y = mx + b)

Este número m se llama pendiente de la recta y es la relación entre la altura y la base, aquí vemos que por cada unidad recorrida en x la recta sube 3 unidades en y por lo que la pendiente es m = 3. & b es el intercepto de la recta con el eje Y (donde la recta se cruza con el eje Y)

Volvamos al ejemplo de las funciones lineales

f(x) = 3x+2 Si x es 3, entonces f (3) = 3*3+2 = 11

Si x es 4, entonces f (4) = 3*4+2 = 14

Si x es 5, entonces f (5) = 3*5+2 = 17

Cada vez que la x se incrementa en 1 unidad, el resultado, esto es, f(x), se incrementa en 3 unidades. Si el valor de la pendiente es positivo la función es Creciente. Preste atención en que los valores de x y de f(x) NO SON PROPORCIONALES.

Lo que son proporcionales son los incrementos.

g(x) = -3x+7 Si x= 0, entonces g (0) = -3*(0) +7 = 0+7 = 7

Si x= 1, entonces g (1) = -3*(1) +7 = -3+7 = 4

Si x= 2, entonces g (2) = -3*(2) +7 = -6+7 = 1

Cada vez que la x se incrementa en 1 unidad, el resultado, esto es, g(x), disminuye en 3 unidades. Si el valor de la pendiente es negativo la función es Decreciente.

h(x) = 4 Si x= 0 , entonces h(0) = 4

Si x= 98 entonces h(98) = 4

Cada vez que la x se incrementa en 1 unidad, el resultado, esto es, h(x), NO aumenta. Es la función constante. Su gráfica es una recta paralela al eje X.

Esta es la representación grafica de los tres tipos de funciones descritas.

Si quieres ampliar estos conceptos te recomiendo estas paginas:

https://es.wikipedia.org/wiki/Funci%C3%B3n_lineal

https://www.x.edu.uy/lineal.htm

https://www.ing.unp.edu.ar/matematica/Modulos/Unidad_4.PDF

Ahora veamos como graficar una función.

z Ejemplos

Representa gráficamente las siguientes funciones lineales y = 2x y y = - 3x + 4

Sugerencia: Primero elabora una tabla de valores, luego ubica los pares de puntos de la tabla en el plano cartesiano y finalmente únelos con una línea recta.

Los valores de x son asignados arbitrariamente o a tu gusto "te aconsejo usar valores pequeños para facilitar las operaciones" luego en la ecuación remplazamos la x por cada valor de la tabla.

1. y = 2x
Vamos a hacerlo con dos valores de x para que sepas de donde salen los valores.

Para x = - 2, y = 2(-2) = -4 quedando la pareja (-2 , -4)

Para x = 1, y = 2(1) = 2 quedando la pareja (1 , 2)

X	*y = 2x*
-2	-4
-1	-2
0	0
1	2
2	4

2. y = - 3x + 4
Vamos a hacerlo con dos valores de x para que sepas de donde salen los valores.

Para x = - 1, y = -3(-1)+ 4 = 7 quedando la pareja (-1 , 7)

Para x = 2, y = -3(2) + 4 = -2 quedando la pareja (2 , -2)

X	*y = - 3x + 4*
-1	7
0	4
1	1
2	-2
3	-5

Ecuaciones lineales

Ecuación lineal con n incógnitas

Una ecuación lineal con n incógnitas es cualquier expresión del tipo: a₁x₁ + a₂x₂ + a₃x₃ + ... + a_nx_n= b, donde a_i, b Pertenece ERRE .

Los valores a_i se denominan coeficientes,

b es el término independiente.

Los valores x_i son las incógnitas.

Solución de una ecuación lineal

Cualquier conjunto de n números reales que verifica la ecuación se denomina solución de la ecuación.

Dada la ecuación x + y + z + t = 0, son soluciones de ella:

(1,-1,1,-1), (-2,-2,0, 4).

Ecuaciones lineales equivalentes

Son aquellas que tienen la misma solución.

x + y + z + t = 0 2x + 2y + 2z + 2t = 0

Ecuaciones lineales de primer grado

Las ecuaciones lineales de primer grado son del tipo ax + b = 0 , con a ≠ 0, ó cualquier otra ecuación en la que al operar, trasponer términos y simplificar adopten esa expresión.

Resolución de ecuaciones de primer grado

En general para resolver una ecuación de primer grado debemos seguir los siguientes pasos:

1º Quitar paréntesis.

2º Quitar denominadores.

3º Agrupar los términos en x en un miembro y los términos independientes en el otro.

4º Reducir los términos semejantes.

5º Despejar la incógnita.

Despejamos la incógnita:

Agrupamos los términos semejantes y los independientes, y sumamos:

Quitamos paréntesis:

Agrupamos términos y sumamos:

Despejamos la incógnita:

Quitamos denominadores, para ello en primer lugar hallamos el mínimo común múltiplo.

Quitamos paréntesis, agrupamos y sumamos los términos semejantes:

Despejamos la incógnita:

Quitamos paréntesis y simplificamos:

Quitamos denominadores, agrupamos y sumamos los términos semejantes:

Quitamos corchete:

Quitamos paréntesis:

Quitamos denominadores:

Quitamos paréntesis:

Agrupamos términos:

Sumamos:

Dividimos los dos miembros por: −9

Fracciones algebraicas

Una fracción algebraica es una expresión fraccionaria en la que numerador y denominador son polinomios.

Son fracciones algebraicas:

$fraccion_algebraica_001$

Las fracciones algebraicas tienen un comportamiento similar a las fracciones numéricas.

El valor de una fracción no se altera si se multiplican o dividen el numerador y denominador por una misma cantidad. Esta cantidad debe ser distinta de cero.

Por ejemplo:

Si $fraccion_alegraica_003$ se multiplica por x + 2 en su numerador y denominador resulta:

$fraccion_alebraica_004$

Se recomienda hacer las operaciones con calma y mucha concentración ya que son frecuentes los errores de signos y los errores en el uso incorrecto de paréntesis.

Operaciones con fracciones algebraicas

Simplificar fracciones algebraicas

La simplificación de fracciones algebraicas es objeto de frecuentes errores, pero se simplifican igual que las fracciones ordinarias: dividiendo el numerador y el denominador por factores comunes. Entonces, la clave está en el factor común. Para simplificar al máximo habrá que factorizar los polinomios numerador y denominador.

Por ejemplo, simplificar:

$fraccion_algebraica_002$

Otro ejemplo, simplificar la fracción

$fraccion_algebraica_005$

Primero, factorizamos los polinomios del numerador y del denominador, para quedar

$fraccion_algebraica_006$

Como vemos, simplificar (o reducir) una fracción algebraica consiste en transformarla a otra equivalente cuya particularidad es ser irreductible (se puede simplificar sólo hasta un cierto nivel).

Suma y resta de fracciones algebraicas

Para sumar y restar procederemos de forma similar a como lo hacemos con fracciones de números enteros, reduciendo primero a común denominador.

Igual como ocurre con las fracciones de números enteros, la suma y resta de fracciones algebraicas puede ser con fracciones de igual denominador o de distinto denominador.

Suma y resta de fracciones algebraicas con igual denominador

Veamos el siguiente ejemplo de suma y resta:

$fraccion_algebraica_007$

Como el denominador es común (x + 1), este se ha unificado en una sola fracción, que ahora tiene como numerador a todas las cantidades que eran numeradores en las fracciones que estamos sumando y restando. Nótese que dichas cantidades se anotan entre paréntesis cuando no son monomios, para no confundir luego los signos.

Ahora sacamos los paréntesis teniendo cuidado de cambiar el signo interior cuando delante del paréntesis hay un signo menos (−), y nos queda

$fraccion_algebraica_008$

Hicimos las operaciones posibles y llegamos al resultado.

Suma y resta de fracciones algebraicas con distinto denominador

Veamos el siguiente ejemplo:

$fraccion_algebraica_009$

Tal como lo hacíamos al sumar o restar fracciones de números enteros, utilizando el mínimo común múltiplo (m.c.m.) las fracciones con distintos denominadores se transforman en fracciones equivalentes con denominador común.

Entonces, que debemos hacer: encontrar el m.c.m. de los denominadores, que llamaremos mínimo común denominador (m.c.d.).

Para calcular el m.c.m. factorizamos

5ab	a²	15b²	a
5b	a	15b²	a
5b	1	15b²	b
5	1	15b	b
5	1	15	5
1	1	3	3
1	1	1

Multiplicamos los factores y queda a • a • b • b • 5 • 3 = a² • b² • 15 que es lo mismo que 15a²b² y es el mínimo común denominador (m.c.d.) de las tres fracciones involucradas.

Conocido el m.c.d. operamos con fracciones con denominador común:

Previamente, dividimos el denominador común (15a²b²) por cada uno de los denominadores individuales, para conocer la cifra o valor que se multiplica por cada uno de los numeradores, y lo hacemos así:

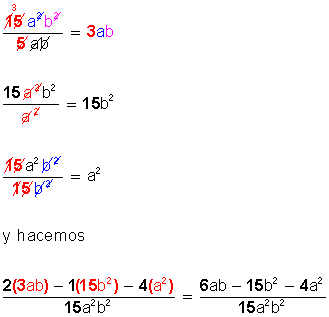
$fracciones_algebraicas_010$

Esta es la forma tradicional de operar cuando hemos hallado el m.c.d. Pero también hay otra, como la siguiente:

Encontrado el m.c.d. (15a²b²) se multiplica cada fracción (tanto numerador como denominador) por los términos que faltan por completar dicho m.c.d., del modo siguiente:

$fraccion_algebraica_011$

Nótese que “los términos que faltan” se obtienen haciendo la misma división del caso anterior.

Un ejemplo más:

Sumar $fraccion_alegeraica_012$

El m.c.m. de los denominadores, o mínimo común denominador (m.c.d.) es x(x − 3)

Hacemos

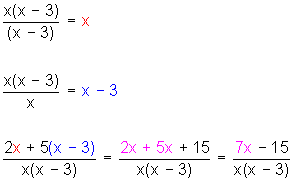
$fraccion_algebraica_013$

¿Qué hicimos? Sumamos los numeradores dejando el mismo denominador y simplificamos el numerador:

Producto (multiplicación) de fracciones algebraicas

Para multiplicar fracciones algebraicas procederemos igual como lo hacemos con fracciones, multiplicando los numeradores y los denominadores, aunque antes de multiplicar debemos simplificar, si se puede.

Veamos qué significa esto:

Sea $fraccion_algebraica_014$ una fracción algebraica cualquiera que está multiplicada por otra $fraccion_algebraica_015$ , entonces: $fraccion_algebraica_016$

Veamos ahora ejemplos de multiplicación (producto) de fracciones algebraicas

Multiplicar

$fraccion_algebraica_017$

Anotamos la multiplicación de los numeradores y de los denominadores:

$fraccion_algebraica_018$

Simplificamos antes de efectuar el producto:

$fraccion_algebraica_019$

Ahora, podemos multiplicar los factores finales:

$fraccion_algebraica_020$

Ejemplos desarrollados

a) $fraccion_algebraica_021$

b) $fraccion_algebraica_022$

c) $fraccion_algebraica_023$

Importante: en los tres ejemplos anteriores (como en casi todos los casos) es preciso dominar la factorización de productos notables.

Cociente o división de fracciones algebraicas

Para dividir fracciones algebraicas procederemos igual como lo hacemos con fracciones, haciendo el producto cruzado de numeradores y denominadores, aunque antes de multiplicar debemos simplificar, si se puede.

Veamos, ahora qué significa esto:

Sea $fraccion_algebraica_014$ una fracción algebraica cualquiera que está dividida por otra $fraccion_algebraica_015$ , entonces:

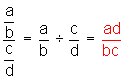
$fraccion_algebraica_024$

Veamos ahora ejemplos de división (cociente) de fracciones algebraicas

Dividir

$fraccion_algebraica_025$

Anotamos haciendo el producto cruzado:

$fraccion_algebraica_026$

Simplificamos y finalmente multiplicamos:

$fraccion_algebraica_027$

Ejemplos desarrollados

a) 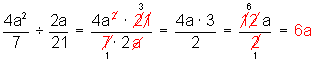$fraccion_algeb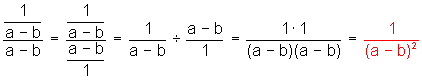raic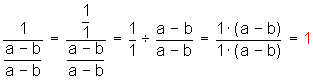a_028$

b) $fraccion_algebraica_029$

c) $fraccion_algebraica_030$

Nota: en ejercicios de este tipo es importante tener bien definida la línea divisoria de las fracciones participantes. Si el ejercicio está bien expresado, la línea divisoria principal es la que se halla frente al signo igual (=).

d) 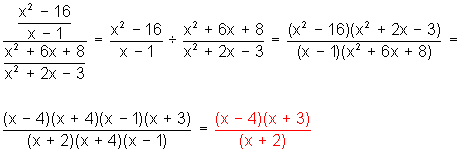$fraccion_algebraica_031$

Fracciones algebraicas compuestas

En los últimos ejemplos nos encontramos con un tipo de fracción algebraica especial: las fracciones compuestas.

Una fracción algebraica compuesta contiene una o varias fracciones simples en el numerador y/o denominador.

La operación de reducción de fracciones compuestas consiste en identificar y reducir las fracciones simples que la componen.

Ejemplos:

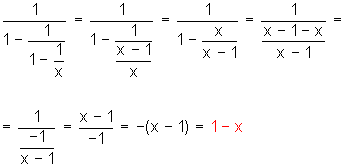
1) $fraccion_algebraica_032$

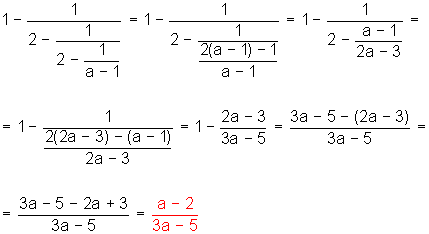
2) $fraccion_algebraica_033$

3) $fraccion_algebraica_034$

la sabiduria esta en el empeño que demuestres

DOCUMENTOS PARA EL CUARTO PERÍODO

PROPIEDADES DE LA POTENCIACIÓN

Multiplicación de potencias de igual base

División de Potencias de Igual Base

Potencia de una potencia

Potencia de un producto

Propiedad distributiva

PUNTO PENDIENTE

PARA RECUPERAR MATEMÁTICAS NECESITAN HACER LO SIGUIENTE:

1. Biografía de los Referentes Matemáticos, Valor 30%:

Elaborar un trabajo en diapositivas (power point) sobre estos matemáticos:

Euler, Gauss, Thales, Jhon Neper

2. Talleres de recuperación de Matemáticas, Valor 40%

TALLERES DE MATEMÁTICAS

3. SUSTENTACIÓN DE LOS TALLERES Y EL TRABAJO. VALOR 30%

DOCUMENTOS NOVENO

Para el tema de sistemas de ecuaciones lineales se recomienda mirar el archivo adjunto.

Sistemas de Ecuaciones Lineales.docx (75,7 kB)

FUNCIÓN LINEAL

Ecuaciones lineales

Ecuación lineal con n incógnitas

Solución de una ecuación lineal

Ecuaciones lineales equivalentes

Ecuaciones lineales de primer grado

Resolución de ecuaciones de primer grado

Fracciones algebraicas

Operaciones con fracciones algebraicas

Ejemplos desarrollados

Ejemplos desarrollados

Menú

Buscar en el sitio

Contacto